Elaboración de grupos de perfiles topográficos, paralelos y de igual longitud

Introducción

Un perfil topográfico corresponde a una relación entre distancia y altitud para una región dada. La gráfica de esta relación permite visualizar la distribución de la altitud a lo largo de una linea o transecto. Se pueden construir perfiles de longitud muy variable y con orientaciones muy diversas.

La selección de la longitud y la orientación de los perfiles a construir está condicionada por el interés del usuario por visualizar la estructura de la distribución de altitudes con respecto a una estructura especifica del relieve. Por ejemplo, puede ser del interés del usuario conocer la morfología de los perfiles topográficos transversales o longitudinales respecto a un valle, a una cadena montañosa o a un tipo de relieve especifico, tal como un bloque tectónico basculado.

En estos casos u otros, el interés reside en conocer la distribución espacial de la altitud en una dirección paralela o transversal a la estructura que se desea estudiar.

Sin embargo, la información que se obtiene utilizando un perfil topográfico único deja una serie de incertidumbres respecto a la distribución de las altitudes en la zona donde se hace el levantamiento; por ejemplo, es factible que el perfil levantado no exprese los valores de altitud máxima o de altitud mínima en la zona de interés. En este caso, solo se tiene certeza de las altitudes máxima y mínima a lo largo del transecto levantado, lo cual no necesariamente corresponde con las altitudes máximas y mínimas de la zona.

El uso de grupos de perfiles paralelos, equidistantes y de la misma longitud permite superar parcialmente las limitaciones inherentes a la construcción de perfiles únicos. Cuando se utilizan conjuntos de perfiles con las características antes mencionadas, se puede conocer toda la información contenida en los perfiles individuales e igualmente elaborar perfiles de altitud máxima, mínima y perfiles de altitud promedia. De este modo, el conocimiento de la distribución espacial de la altitud a lo largo de transectos brinda información complementaria útil para asociar al estudio de las estructuras de interés por parte del usuario.

El uso de conjuntos de perfiles se aplica en dos casos distintos:

  1. El altiplano de Santa Rosa de Osos en la parte norte de la cordillera Central presenta una expresión morfológica clara de un bloque tectónico basculado al sureste. Con un sistema de perfiles longitudinales orientados en el sentido del basculamiento se busca hacer explicito este fenomeno. Igualmente se construye otro conjunto de perfiles transversales para visualizar los efectos morficos de redes de drenaje.

  2. El segundo ejemplo consiste en trazar perfiles transversales al cañón del río Medellín entre Copacabana y Barbosa para hacer explicita la relación espacial entre cañones lineales y altiplanos en la zona central de Antioquia.

Objetivos

  • Desarrollar un procedimiento para la elaboración de conjuntos de perfiles topográficos paralelos, equidistantes y de igual longitud combinando GRASS y R.
  • Construir perfiles de altitud máxima, mínima y promedia para la franja de transecto seleccionada.
  • Interpretar la distribución de la altitud en la zona seleccionada.

Procedimiento

  • Definir una linea de referencia que contiene los puntos iniciales de los diversos perfiles a construir. Esta linea debe ser transversal a la estructura o relieve a estudiar, si el conjunto de perfiles a construir corresponde a perfiles longitudinales.
  • Identificar y ubicar los puntos de partida de los perfiles a levantar.
  • Definir y construir el conjunto de perfiles.

Desarrollo

Se debe descargar e importar el mapa raster de altiplanos (recordar el procedimiento explicado en la Clase 10).

Importar el nuevo mapa al location CursoGrass

Debemos ubicarnos en el directorio donde se encuentre el archivo altiplanos.tif utilizando el comando cd.

cd Downloads
r.in.gdal input=altiplanos.tif output=altiplanos

Desplegar un mapa raster del altiplano y dibujarle una cuadrícula densa

Una vez importado el mapa, verificamos que este se encuentre en la lista de mapas raster disponibles en GRASS, y procedemos a establecer la región de manera apropiada para poderlo desplegar en su totalidad.

g.list rast
g.region -p rast=altiplanos
d.mon x0
d.rast altiplanos
d.grid help
d.grid size=2000

Como el mapa aún no tiene tabla de colores, creamos una que permita visualizar los rasgos del relieve de una manera más agradable:

TC_altiplanos

 750  85 128  64 # Verde oscuro
2200 159 217 130 # Verde claro
2300 178  34  34 # Firebrick
2500 236 142 142 # Rojo claro
2800 139  69  19 # Saddle brown
3350 245 245 220 # Beige

Aplicamos la tabla de colores nueva y volvemos a desplegar el mapa. Para dibujar la cuadrícula utilizamos el comando d.grid especificándole la densidad con el parámetro size.

r.colors map=altiplanos rules=TC_altiplanos
d.rast altiplanos
d.grid size=2000

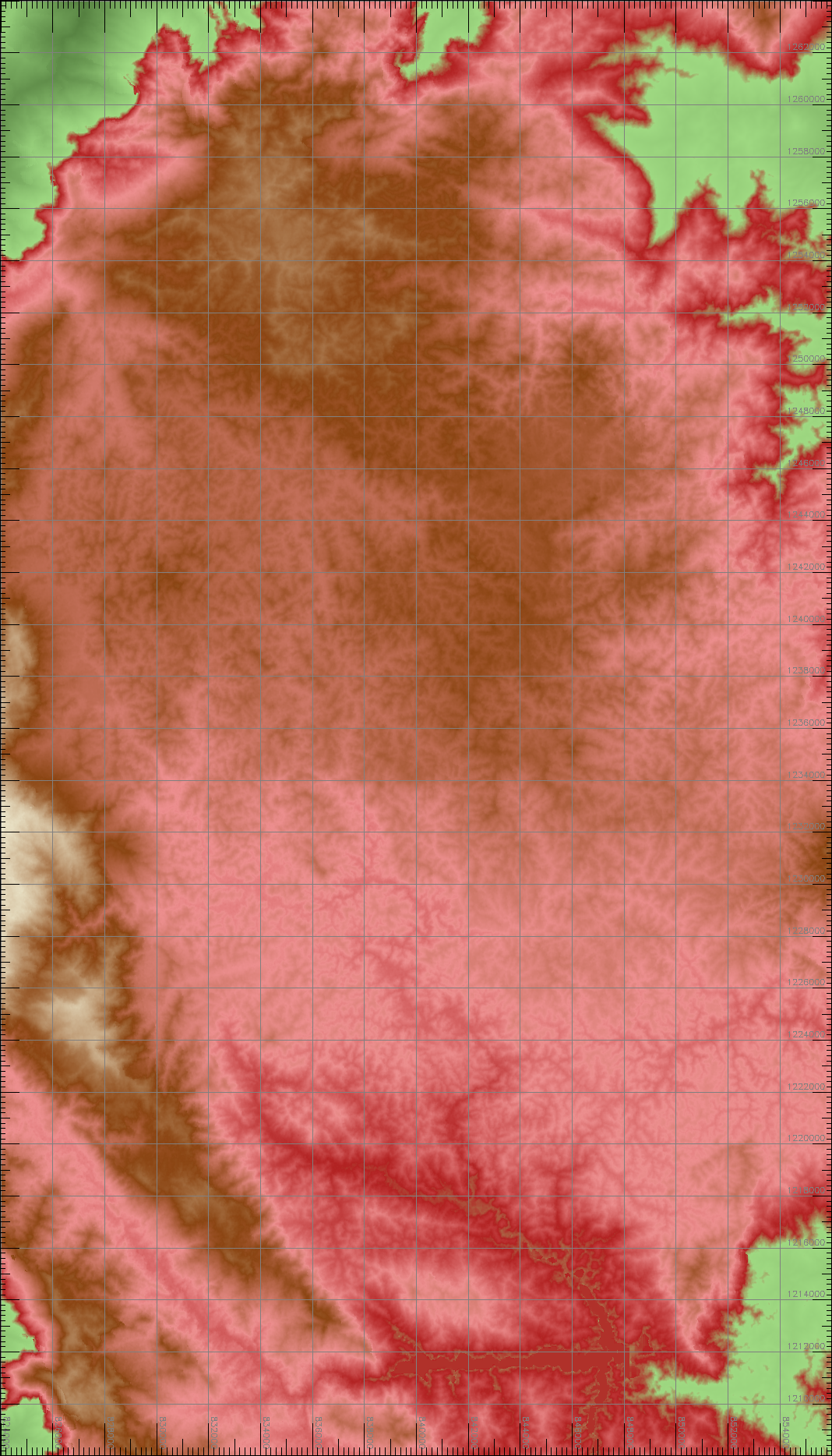
Altiplanos

Obtener un archivo con los datos del perfil transversal al conjunto de perfiles a levantar

Se emplea el comando r.profile para generar un primer perfil transversal a la estructura de basculamiento que se quiere estudiar. A partir del perfil transversal, se construirán los diferentes perfiles longitudinales paralelos a la estructura de basculamiento.

Se utiliza el comando v.in.ascii para generar el perfil en formato vectorial.

Podemos utilizar el redireccionador | para que la salida de un comando sea la entrada del siguiente:

r.profile -g input=altiplanos profile=839954.615861,1212011.820184,855220.587482,1223332.652859 | v.in.ascii out=perfil_transversal fs=space

Perfil transversal generado

Seleccionar a lo largo del perfil transversal, los puntos iniciales de los perfiles longitudinales

El perfil transversal tiene una longitud de 18990 m. Vamos a tomar puntos equidistantes cada 1 km a partir de los 10 km de distancia en este perfil.

Los puntos seleccionados son:

847978.956746 1217962.454886 9990.000000 2489
848798.258819 1218570.027198 11010.000000 2474
849593.463771 1219159.729736 12000.000000 2482
850388.668724 1219749.432274 12990.000000 2497
851207.970796 1220357.004586 14010.000000 2486
852003.175749 1220946.707124 15000.000000 2488
852798.380701 1221536.409662 15990.000000 2479
853617.682774 1222143.981974 17010.000000 2494
854412.887726 1222733.684512 18000.000000 2499
855208.092679 1223323.387050 18990.000000 2515

Observar que el valor de distancia seleccionado sólo en algunos casos coincide exáctamente. Como la resolución espacial es de 30 m, entonces tenemos valores cerrados de distancia para 12 km, 15 km y 18 km; este pequeño desfase no tiene ninguna implicación respecto a los valores de altitud que son constantes para el pixel de 30 m x 30 m.

Calcular el azimuth del perfil transversal

Empleando el punto inicial (847978.956746 1217962.454886) y el punto final (855208.092679 1223323.387050) de los puntos seleccionados, se calcula la distancia W-E y la distancia N-S, entre estos 2 puntos extremos.

\[\begin{align} \Delta_{x} &=& 855208.092679 - 847978.956746 &=& 7229.135933 \\ \Delta_{y} &=& 1223323.387050 - 1217962.454886 &=& 5360.932164 \\ & & \tan(\theta) = \frac{\Delta_{y}}{\Delta_{x}} = \frac{5360.932164}{7229.135933} &=& 0.74157302 \\ & & \theta = \tan^{-1}(0.74157302) &=& 36.6° \\ \end{align}\]

El perfil transversal hace un ángulo de 36.6° con el eje W-E. El azimuth medido deesde el eje N-S es:

\[90° - 36.6° = 53.4°\]

Parámetros para construir los perfiles longitudinales con la estructura a explorar

Se utiliza el comando r.transect para construir los perfiles. Este comando requiere el nombre del mapa de donde se extraerá la información. Igualmente se requiere precisar los parámetros de la linea del perfil a construir. Estos parámetros son:

  • Coordenadas del punto inicial del perfil.
  • El azimuth de la linea.
  • Longitud del perfil.

El mapa de donde se extraen los perfiles es altiplanos.

Las coordenadas de los puntos iniciales se obtuvieron en el procedimiento precedente.

El azimuth de los perfiles longitudinales es perpendicular al azimuth del perfil transversal. Por lo tanto su valor es de:

\[360° - 36.6° = 323.4°\]

Construcción individual de los perfiles longitudinales

Los parámetros son:

  • El azimuth de los perfiles longitudinales es: 323.4°
  • La longitud de los perfiles es de 25000 metros.
  • Los puntos iniciales de los nueve perfiles se tienen del perfil transversal.
r.transect -g  map=altiplanos line=847978.956746,1217962.454886,323.4,25000 | v.in.ascii output=perfil1 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=848798.258819,1218570.027198,323.4,25000 | v.in.ascii output=perfil2 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=849593.463771,1219159.729736,323.4,25000 | v.in.ascii output=perfil3 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=850388.668724,1219749.432274,323.4,25000 | v.in.ascii output=perfil4 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=851207.970796,1220357.004586,323.4,25000 | v.in.ascii output=perfil5 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=852003.175749,1220946.707124,323.4,25000 | v.in.ascii output=perfil6 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=852798.380701,1221536.409662,323.4,25000 | v.in.ascii output=perfil7 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=853617.682774,1222143.981974,323.4,25000 | v.in.ascii output=perfil8 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=854412.887726,1222733.684512,323.4,25000 | v.in.ascii output=perfil9 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'
r.transect -g  map=altiplanos line=855208.092679,1223323.387050,323.4,25000 | v.in.ascii output=perfil10 fs=space columns='coord_x double precision, coord_y double precision, distancia double precision, altitud int'

Se emplea el comando v.in.ascii de manera similar al perfil transversal, para generar los perfiles topográficos como mapas vectoriales de GRASS.

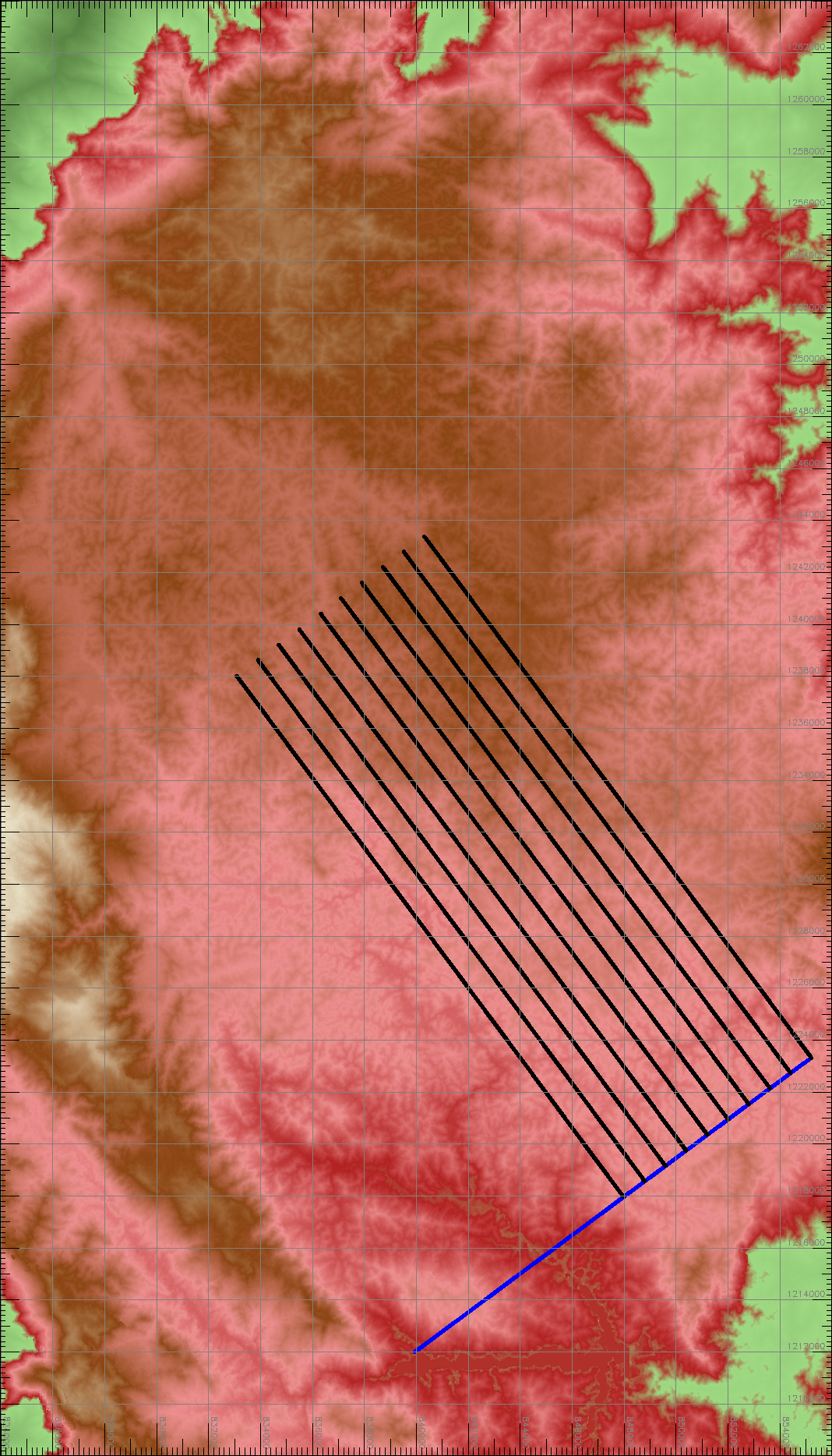
Perfiles longitudinales

Luego con el comando db.describe -c comprobamos que cada uno de los perfiles construidos contenga cinco columnas, y lo más importante, un número igual de filas:

db.describe -c perfil1
db.describe -c perfil2
db.describe -c perfil3
db.describe -c perfil4
db.describe -c perfil5
db.describe -c perfil6
db.describe -c perfil7
db.describe -c perfil8
db.describe -c perfil9
db.describe -c perfil10

Comprobamos que cada perfil contiene 834 puntos.

Las columnas de cada perfil son:

  • cat
  • coord_x
  • coord_y
  • distancia
  • altitud

Transferir la información vectorizada de los perfiles desde GRASS a R

Estando en GRASS desde el mapset donde se tienen los perfiles se entra a R.

R

Para iniciar procedimientos en R utilizando la información que se encuentra en GRASS, es necesario cargar la biblioteca spgrass6, el cual permite esta conexión.

library(spgrass6)

Observar que al cargar la biblioteca, esta indica que se ha cargado GRASS GIS desde el location CursoGrass.

Cargar y consultar los perfiles en R

Se utiliza la función readVECT6 de la biblioteca spgrass6, que permite leer los mapas vectoriales del location actual. Esta función genera un objeto de puntos espaciales (SpatialPointsDataFrame), del cual para efectos de este ejercicio, sólo nos interesa la base de datos, lo cual indicamos con @data.

perfil1 <- readVECT6("perfil1")@data
str(perfil1)

Utilizamos la función str para consultar la estructura de la base de datos y constatamos que es la misma que teníamos en GRASS.

Repetir el procedimiento para los demás perfiles:

perfil2 <- readVECT6("perfil2")@data
perfil3 <- readVECT6("perfil3")@data
perfil4 <- readVECT6("perfil4")@data
perfil5 <- readVECT6("perfil5")@data
perfil6 <- readVECT6("perfil6")@data
perfil7 <- readVECT6("perfil7")@data
perfil8 <- readVECT6("perfil8")@data
perfil9 <- readVECT6("perfil9")@data
perfil10 <- readVECT6("perfil10")@data

Graficar varios perfiles en un solo gráfico

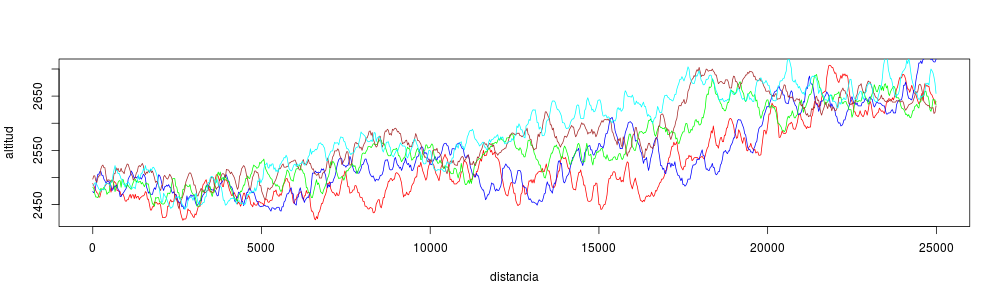
Para graficar los primeros 5 perfiles, empleamos la función plot para el primer perfil, y la función points para los restantes 4 perfiles. Se utiliza el parámetro type para que los puntos sean graficados como una línea, y el parámetro col para el color.

with(perfil1, plot(distancia, altitud, type="l", col="red"))
with(perfil2, points(distancia, altitud, type="l", col="blue"))
with(perfil3, points(distancia, altitud, type="l", col="green"))
with(perfil4, points(distancia, altitud, type="l", col="brown"))
with(perfil5, points(distancia, altitud, type="l", col="cyan"))

Perfiles altiplano

Construcción de la matriz de altitudes

  • Se elaboran los vectores que contienen los valores de altitud.
Hperfil1 <- perfil1$altitud
Hperfil2 <- perfil2$altitud
Hperfil3 <- perfil3$altitud
Hperfil4 <- perfil4$altitud
Hperfil5 <- perfil5$altitud
Hperfil6 <- perfil6$altitud
Hperfil7 <- perfil7$altitud
Hperfil8 <- perfil8$altitud
Hperfil9 <- perfil9$altitud
Hperfil10 <- perfil10$altitud
  • Los vectores anteriores se combinan de tal modo que queden como columnas para elaborar una matriz de altitudes de los perfiles seleccionados utilizando la función cbind.
MHperfiles <- cbind(Hperfil1, Hperfil2, Hperfil3, Hperfil4, Hperfil5,
                    Hperfil6, Hperfil7, Hperfil8, Hperfil9, Hperfil10)
  • Verificamos las dimensiones de la matriz utilizando la función dim.
dim(MHperfiles)

La matriz obtenida tiene 834 filas y 10 columnas.

  • Cada columna contiene los valores de altitud de cada uno de los perfiles levantados.
head(MHperfiles)

Obtener los valores máximo, mínimo y promedio de cada fila de la matriz

Altitudes máximas

Para calcular el valor de altitud máxima de cada fila se utiliza la función apply.

apply(MHperfiles, 1, max)

Este cálculo permite obtener 834 valores de altitud máxima, uno para cada fila de la matriz.

Para llevar los valores obtenidos como una nueva columna de la matriz:

MHperfiles <- cbind(MHperfiles, apply(MHperfiles, 1, max))
head(MHperfiles)

Observar que la primera version de la matriz contiene diez columnas y la segunda contiene once columnas. Esta onceava columna corresponde a los valores de altitud máxima en cada fila. Pero la columna carece de nombre.

Con la función colnames se le asigna el nombre Hmax a la columna 11 de la matriz.

colnames(MHperfiles)[11] <- "Hmax"
head(MHperfiles)

Altitudes promedio

MHperfiles <- cbind(MHperfiles, apply(MHperfiles, 1, mean))
colnames(MHperfiles)[12] <- "Hmean"
head(MHperfiles)

Altitudes mínimas

MHperfiles <- cbind(MHperfiles, apply(MHperfiles, 1, min))
colnames(MHperfiles)[13] <- "Hmin"
head(MHperfiles)

En el trabajo precedente se construyó una matriz de altitudes con diez perfiles; luego se calcularon los valores de altitud máxima, promedio y mínima para cada fila de la matriz. Finalmente se tiene una matriz de 13 columnas y 834 filas.

dim(MHperfiles)

Graficar la matriz obtenida

Graficar todos los perfiles

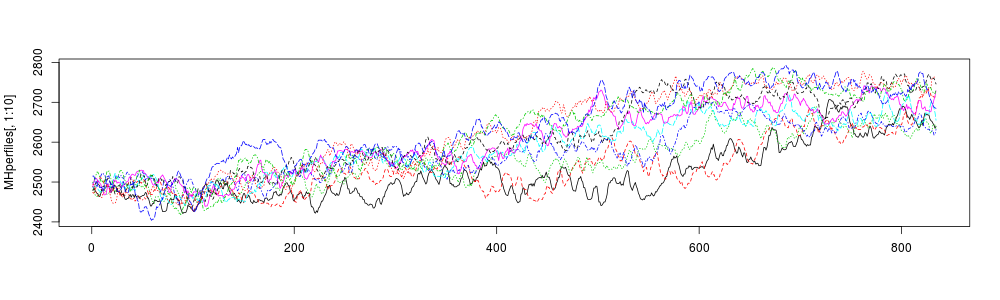
Seleccionamos únicamente las primeras 10 columnas, las cuales corresponden a los perfiles topográficos levantados.

matplot(MHperfiles[,1:10], type = "l")

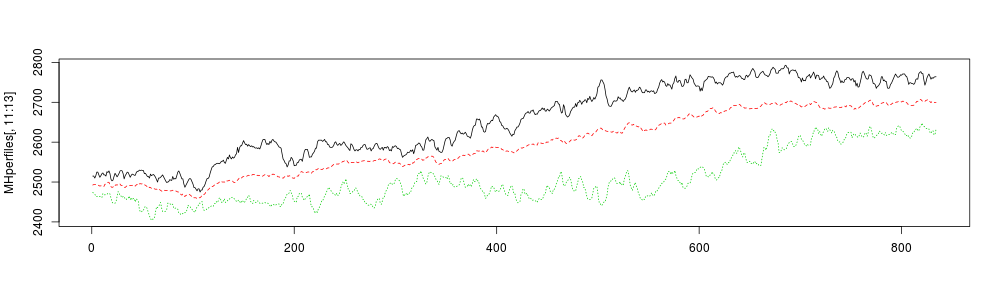
Graficar altitudes máximas, promedio y mínimas

matplot(MHperfiles[,11:13], type = "l")

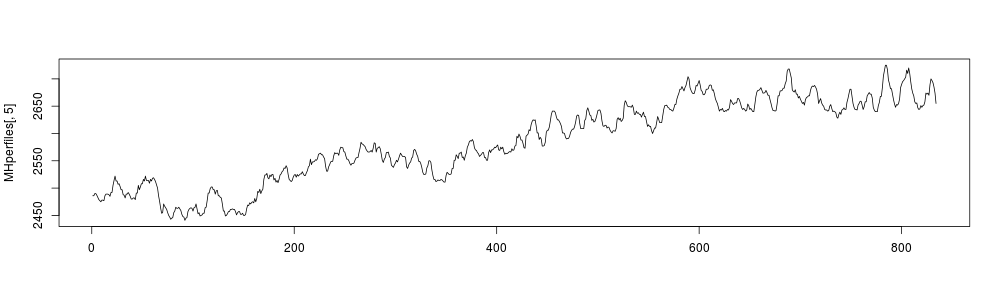
Graficar un perfil específico

Se selecciona el número de la columna correspondiente al perfil que se quiera graficar.

matplot(MHperfiles[,5], type = "l", lwd = 2, col = "blue", main = "Perfil No. 5")

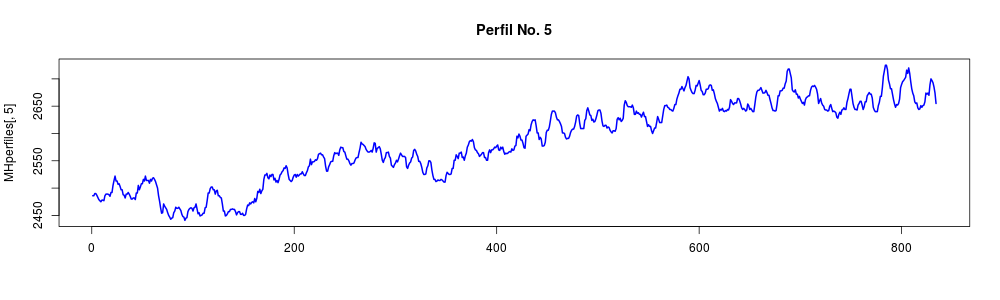
Personalizar un poco la gráfica obtenida

  • Si se quiere modificar el grosor de la línea, se utiliza el parámetro lwd.
  • Para cambiar el color de la línea, se utiliza el parámetro col.
  • Si se quiere modifcar el título, se utiliza el parámetro main.
  • Si se desean agregar etiquetas a los ejes, se pueden utilizar los parámetros xlab y ylab.
matplot(MHperfiles[,5], type = "l", lwd = 2, col = "blue", main = "Perfil No. 5")

Agregar distancias a la matriz de altitudes

En los ejemplos precedentes el eje X representa la secuencia de puntos dentro del perfil; por eso los valores van desde 0 hasta 834.

Para tener un eje X con distancias en metros, se incorpora una primera columna de distancias y se le asigna el nombre.

MHperfiles <- cbind(perfil1$distancia, MHperfiles)
colnames(MHperfiles)[1] <- "Distancia"

Volvemos a graficar las altitudes máximas, mínimas y promedios, pero utilizando la distancia en el eje horizontal. Utilizamos la función legend para ubicar una leyenda en el gráfico.

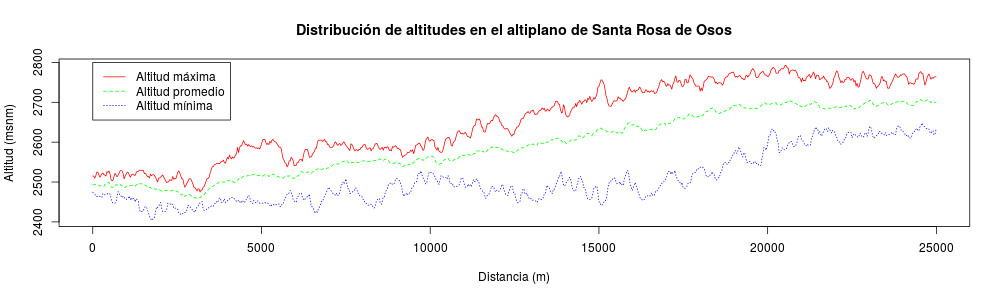
matplot(x = MHperfiles[,1], y = MHperfiles[,12:14], type = "l", col = c("red", "green", "blue"),
        main = "Distribución de altitudes en el altiplano de Santa Rosa de Osos",
        xlab = "Distancia (m)", ylab = "Altitud (msnm)")
legend(0, 2800, c("Altitud máxima", "Altitud promedio", "Altitud mínima"),
       col = c("red", "green", "blue"), lty = 1:3)