Un parámetro importante en la descripción cuantitativa del relieve es la pendiente. Con base en un mapa raster de altitudes (DSM o DTM) se puede calcular un mapa raster de pendiente; en este caso, se asigna un valor de pendiente a cada píxel.
La pendiente y otros parámetros útiles se pueden calcular haciendo uso de la herramienta r.param.scale, que abrimos desde el menú Raster -> Terrain analysis -> Terrain parameters.
Se abre la ventana de la herramienta de parámetros morfométrios en la cual podemos extraer parámetros del terreno a partir de un DEM, es decir que como mapa de entrada tendremos nuevamente a porcecito.
Parámetros que se pueden calcular a partir del DEM
elev: Las elevaciones vienen con el mapa DEM, este parámetro se utiliza para repetir el muestreo a diferente escala.
slope: Calcula la magnitud de la gradiente máxima (el angulo de mayor inclinación de la vertiente, en un punto o píxel. La pendiente en un archivo raster se calcula como la mayor gradiente que se obtiene interpolando el píxel central con los ocho (8) píxeles adyacentes cuando se utiliza una ventana móvil de 3 x 3 píxeles.
aspect: Corresponde a la dirección o azimuth de la gradiente máxima. Se proyecta el vector de la gradiente máxima en el plano horizontal y el valor del azimuth de esta proyección constituye el valor del “aspect”.
- El valor del aspect varia de 0° a +180° cuando se va del Oeste al Norte y al Este.
- El valor del aspect varia de 0° a -180° cuando se va del Oeste al Sur y al Este.
profc: Curvatura del perfil (curvatura que intersecta con el plano definido por el eje Z y la dirección de la gradiente máxima). Corresponde a la curvatura vertical del perfil en el sentido de la pendiente. El “profc” corresponde a la linea de interceptación entre:
- Un plano vertical que contiene a los vectores “slope” y “aspect”.
- La superficie curva del píxel.
- Los valores positivos de profc hacen referencia a una curvatura convexa.
- Los valores negativos de profc hacen referencia a una curvatura cóncava.
- Los valores de cero (0) para profc hacen referencia a una superficie planar.
planc: Curvatura plana (curvatura horizontal, que intersecta con el plano XY). Corresponde a la curvatura horizontal. La curvatura planc es la linea de interceptación entre:
- Un plano horizontal que pasa por el píxel i
- La superficie curva del píxel.
- El signo de esta curvatura tiene significados contrarios a los de profc, es decir:
- Los valores positivos de planc hacen referencia a una curvatura cóncava.
- Los valores negativos de planc hacen referencia a una curvatura convexa.
- Los valores de cero (0) para planc hacen referencia a una superficie planar.
Para Wood, J.D. (1996); las curvaturas del perfil (profc) y la curvatura horizontal (planc) “son útiles en tanto ellas separan la curvatura en dos componentes ortogonales donde los efectos de del proceso gravitacional se maximizan en un caso (profc) o se minimizan en el otro (planc)”.
longc: Curvatura longitudinal (curvatura de perfil que intersecta con el plano definido por la superficie normal y la dirección de la gradiente máxima).
crosc: Curvatura transversal (curvatura tangencial que intersecta con el plano definido por la superficie normal y una tangente al contorno - perpendicular a la dirección de la gradiente máxima).
maxic: Curvatura máxima (en cualquier dirección).
minic: Curvatura mínima (en dirección perpendicular a la dirección de la curvatura máxima).
feature: Características morfométricas:
- Peak: Punto en una convexidad local en todas las direcciones.
- Ridge: Punto en una convexidad local ortogonal a una línea sin convexidad o concavidad.
- Pass: Punto en una convexidad local ortogonal a una concavidad local.
- Plane: Puntos que se encuentran en una superficie sin convexidad o concavidad.
- Channel: Punto en una concavidad local ortogonal a una línea sin convexidad o concavidad.
- Pit: Punto en una concavidad local en todas las direcciones.
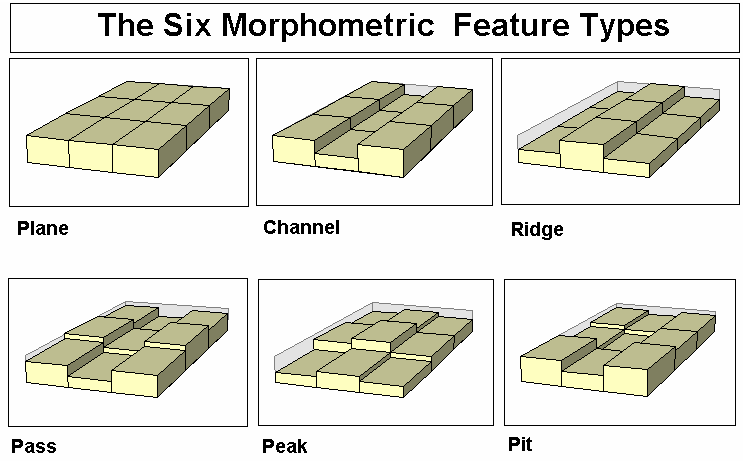
Elaboración de un mapa de pendientes
Conceptos importantes:
La pendiente es la variación de la altitud con respecto a la distancia.
- ¿Qué es una vertiente?
- ¿Cuáles son los limites de las vertientes?
- Relación de la vertiente con otros atributos de estructura y dinámica del relieve.
- Con la litología.
- Con la erosión.
- Con los movimientos en masa (caídas, volcamientos, deslizamientos, flujos).
- Relación de la pendiente de la vertiente con las intervenciones y su aprovechamiento:
- Viviendas y edificaciones.
- Construcción de redes viales.
- Relación de la pendiente de la vertiente con la distribución de la cobertura vegetal natural y cultivada.
- ¿Existe alguna relación?
- ¿Se trata de una relación directa o de una relación indirecta?
¿Cómo elaborar el mapa de pendientes de una región con significados importantes respecto a la dinámica e intervención del relieve?
Se trata de seleccionar unos rangos de pendiente que guarden relación con fenómenos naturales, fenómenos inducidos por la intervención o con ciertos factores limitantes o favorables a una intervención antrópica pertinente técnica y ambientalmente.
Por ejemplo, supongamos que se va intervenir en una región amplia con diversas actividades agropecuarias, forestales y de conservación; para hacerlo será necesario igualmente desarrollar algunas obras de infraestructura tales como vías, viviendad y otras construcciones. ¿Qué servicio puede brindar la elaboración de un mapa de pendientes a este programa?
Las tierras con pendientes muy suaves (< 1°-2°) podrían ser susceptibles a inundación permanente o temporal si se ubican en áreas adyacentes a corrientes de agua (en las llanuras aluviales de los ríos). Estos mismos terrenos podrían albergar un recurso suelo óptimo para actividad agropecuaria.
Un reconocimiento general de la región de interés podría indicar que las manifestaciones de deslizamientos activos y deslizamientos pasados ocurren en vertientes con un umbral mínimo de pendiente. A modo de ejemplo, que se pueda firmar: los deslizamientos se presentan en vertientes con valores de pendiente por encima de los 25°.
Que exista una norma ambiental que afirme por ejemplo: queda prohibido construir viviendas en vertientes con pendientes por encima de los 21°.
Que los ganaderos y las instituciones de este sector consideren inadecuado establecer sistemas de rotación de potreros en vertientes con pendientes por encima de los 13°.
Que los ingenieros afirmen que resulta demasiado costos construir la red vial en vertientes con inclinaciones superiores a 30°.
Con toda esta información se pueden establecer unos posibles rangos, cuya validez es solamente para la región del proyecto:
| Pendiente | Descripción |
|---|---|
| 0° - 1° | Terrenos susceptibles a inundación |
| 1° - 2° | Terrenos susceptibles a inundación temporal (drenan fácilmente una vez desciende el nivel del río) |
| 2° - 13° | ??? |
| 13° - 21° | ??? |
| 21° - 25° | ??? |
| 25° - 30° | ??? |
| >30 | ??? |
¿Qué se puede afirmar acerca de los últimos cinco (5) rangos de pendiente en la tabla anterior?
Procedimiento en GRASS
Haciendo uso de la herramienta r.param.scale vamos a indicar un nombre descriptivo para el mapa que obtendremos, haciendo referencia al parámetro y al tamaño de la ventana móvil de procesamiento.
En la pestaña Optional indicamos el parámetro a extraer y el tamaño de la ventana móvil a utilizar. Empleamos el tamaño por omisión que utiliza el comando (3 x 3).
Y construimos el mapa de pendientes.
Visualizamos el mapa de pendientes:
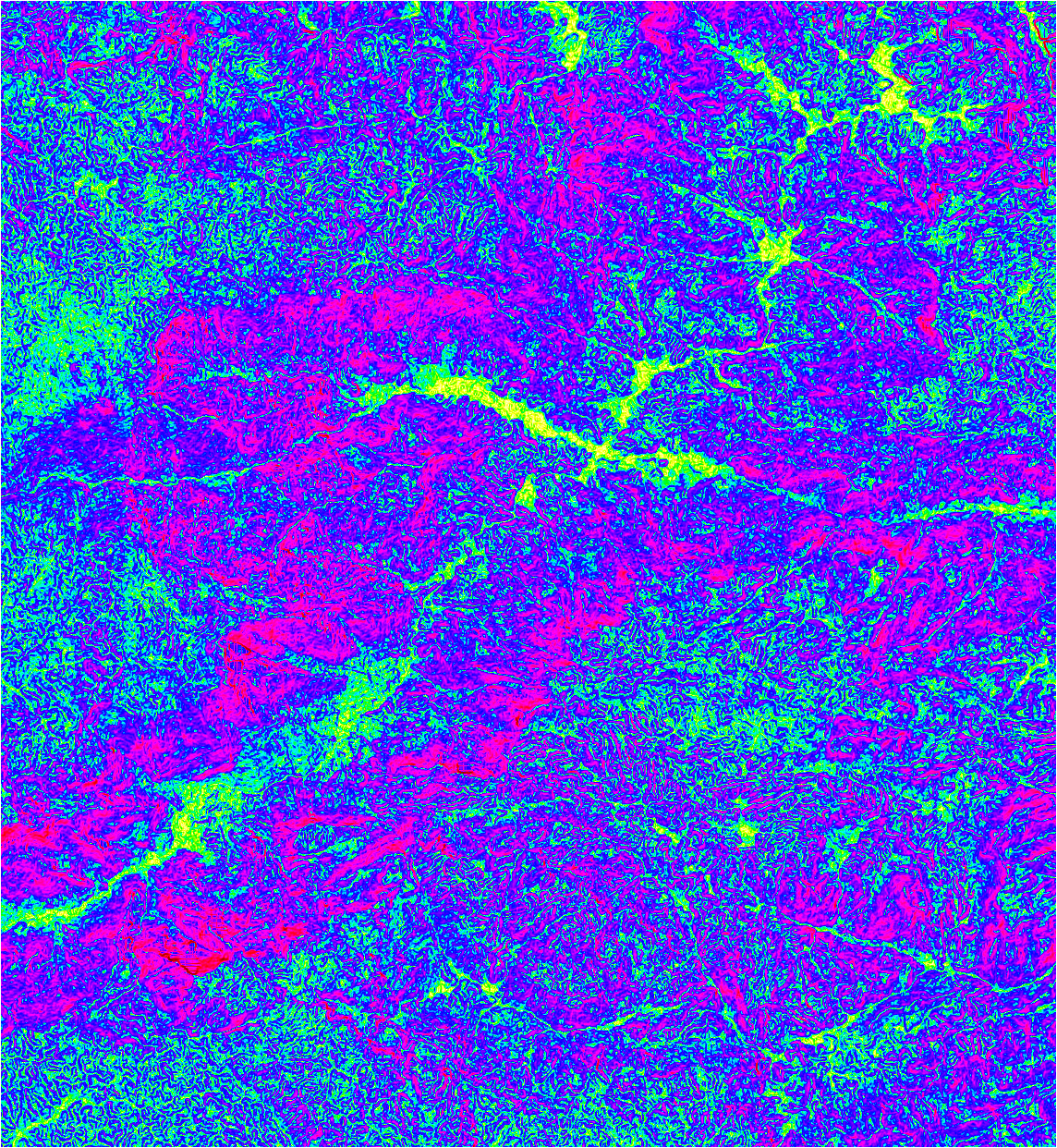
Contestar los siguientes interrogantes:
- ¿En qué parte del relieve se ubican las pendientes mas fuertes y que valores despliegan?
- ¿En qué parte del relieve se ubican las pendientes mas suaves y que valores despliegan?
- ¿Cuáles son las pendientes predominantes en la región de porcecito?
Estadísticos básicos del mapa de pendientes:
total null and non-null cells: 1420848
total null cells: 4768
Of the non-null cells:
----------------------
n: 1416080
minimum: 0
maximum: 71.7685
range: 71.7685
mean: 17.2661
mean of absolute values: 17.2661
standard deviation: 8.03757
variance: 64.6026
variation coefficient: 46.5511 %
sum: 24450217.7022213
Construir el histograma de las gradientes
Utilizar la herramienta de histograma 
del visualizador de mapas para ver un histograma continuo de los valores:
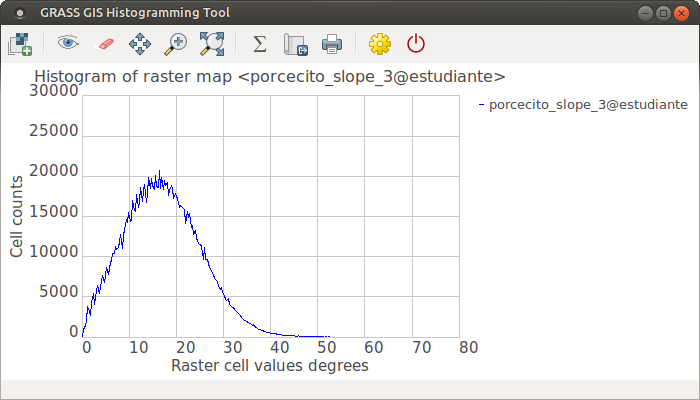
¿Cómo interpretar el histograma?
Reclasificar el mapa de pendientes
Utilizando el mismo procedimiento que utilizamos para reclasificar el mapa de relieve relativo, elaboramos una tabla de reclasificación de la pendiente y la iremos modificando para obtener una representación categórica que nos satisfaga.
Con seis categorías: Mapa 1
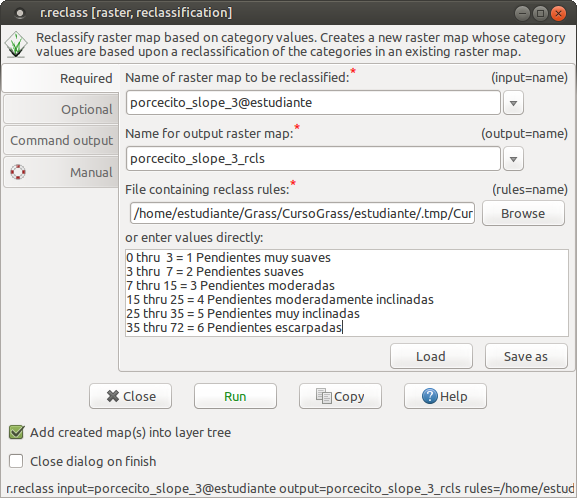
0 thru 3 = 1 Pendientes muy suaves
3 thru 7 = 2 Pendientes suaves
7 thru 15 = 3 Pendientes moderadas
15 thru 25 = 4 Pendientes moderadamente inclinadas
25 thru 35 = 5 Pendientes muy inclinadas
35 thru 72 = 6 Pendientes escarpadas
La reclasificación de la pendiente en 6 rangos con los límites antes anotados genera un mapa de “sal y pimienta”.
Vamos a hacer una reclasificación más simple solo con tres categorías.
Con tres categorías: Mapa 2
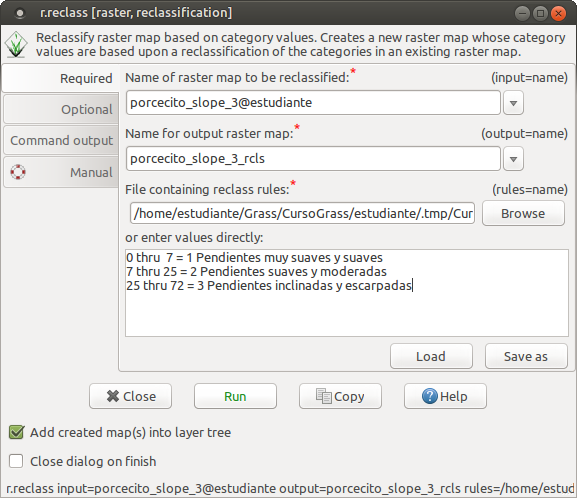
0 thru 7 = 1 Pendientes muy suaves y suaves
7 thru 25 = 2 Pendientes suaves y moderadas
25 thru 72 = 3 Pendientes inclinadas y escarpadas
El mapa con 3 categorías se torna más claro que el mapa con 6 categorías. Es frecuente que el excesivo detalle en la reclasificación de mapas no permite ver los patrones más frecuentes porque pasan desapercibidos debido a una excesiva reclasificación.
Con tres categorías pero modificando sus límites: Mapa 3
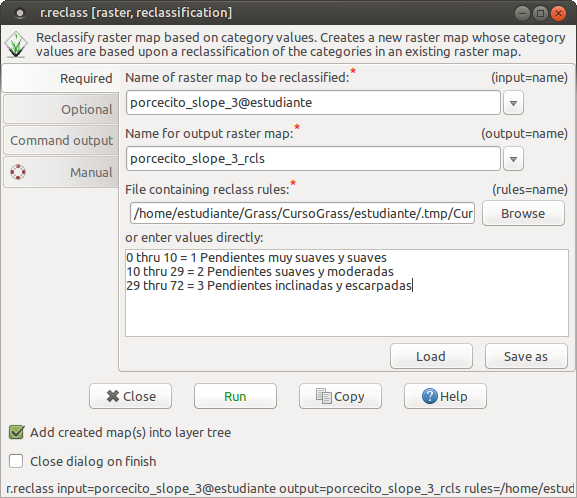
0 thru 10 = 1 Pendientes muy suaves y suaves
10 thru 29 = 2 Pendientes suaves y moderadas
29 thru 72 = 3 Pendientes inclinadas y escarpadas
¿Cuáles son las diferencias mas importantes entre los tres mapas?
¿Qué características del terreno resaltan en un mapa que aparecen poco evidentes claras en otro?
Consultar la información del mapa reclasificado de la pendiente
Si obtenemos un reporte del mapa reclasificado de pendientes obtendremos la siguiente tabla.
+-----------------------------------------------------------------------------+
| Category Information | square | cell| % |
|#|description |kilometers| count| cover|
|-----------------------------------------------------------------------------|
|1|Pendientes muy suaves y suaves . . . . . . . . . | 234.27038| 250921| 17.66|
|2|Pendientes suaves y moderadas. . . . . . . . . . | 972.56924|1041694| 73.31|
|3|Pendientes inclinadas y escarpadas . . . . . . . | 115.27211| 123465| 8.69|
|*|no data. . . . . . . . . . . . . . . . . . . . . | 4.45160| 4768| 0.34|
|-----------------------------------------------------------------------------|
|TOTAL |1326.56333|1420848|100.00|
+-----------------------------------------------------------------------------+
Observemos que aparece una categoría para los valores no data. Esto se debe al efecto de borde, pues en los pixeles del borde del mapa no habrá un valor de pendiente.
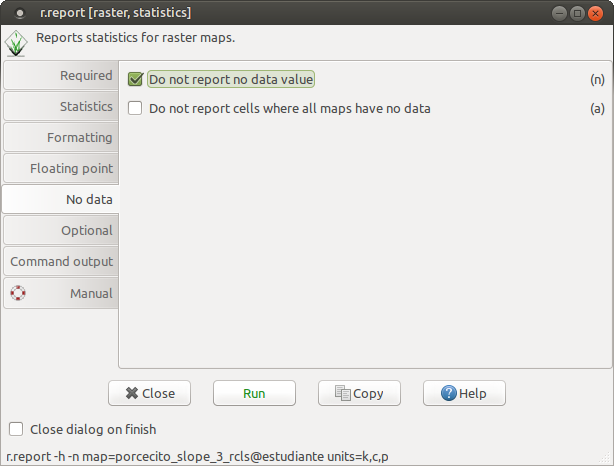
Para omitir los pixeles nulos del reporte utilizamos la opción de no reportar los valores sin datos (nulos) de la pestaña No data de la herramienta r.report.
+-----------------------------------------------------------------------------+
| Category Information | square | cell| % |
|#|description |kilometers| count| cover|
|-----------------------------------------------------------------------------|
|1|Pendientes muy suaves y suaves . . . . . . . . . | 234.27038| 250921| 17.72|
|2|Pendientes suaves y moderadas. . . . . . . . . . | 972.56924|1041694| 73.56|
|3|Pendientes inclinadas y escarpadas . . . . . . . | 115.27211| 123465| 8.72|
|-----------------------------------------------------------------------------|
|TOTAL |1322.11173|1416080|100.00|
+-----------------------------------------------------------------------------+
Actividad extra-curso
- Colocarle variación gradual del color al mapa de pendientes de porcecito.
- Emplear tabla gradacional de los colores que empleó para asignar colores al mapa reclasificado de pendientes.
- ¿Qué diferencias importantes observa entre los dos mapas cuando lo observa en 2D y en 3D?
- Realice una amplación de ambos mapas para observar con mas detalle algunos sectores de los mapas y facilitar el análisis comparativo.
Clasificación de las vertientes según su curvatura
Conceptos importantes:
Digamos que un atributo necesario pero no suficiente de una vertiente es el de poseer extensión.
Las vertientes son superficies modeladas por procesos de remoción.
- A las vertientes como superficies se les puede calcular perfiles.
- Los perfiles son lineas.
- Los perfiles se obtienen de graficar “distancia vs altitud”.
- Los perfiles de los terrenos son lineas muy irregulares que resultan de unas combinaciones complejas de tres tipos de segmentos básicos: convexo (X), cóncavo (V) y rectilíneo (R).
- La gradiente es la variación de la altitud con respecto a la distancia.
- La variación de la gradiente con respecto a la distancia define el carácter convexo, cóncavo o rectilíneo de un segmento del perfil.
Recordar del mapa de pendientes que se estableció que la pendiente es la variación de la altitud con respecto a la distancia.
Ahora, la curvatura es la variación de la pendiente con respecto a la distancia.
Un incremento sostenido de la pendiente con respecto a la distancia genera una curvatura convexa.
Una disminución sostenida de la pendiente con respecto a la distancia genera una curvatura cóncava.
Para definir la forma de una superficie se emplean dos perfiles ortogonales: uno en el sentido de la dirección de la superficie y otro en el sentido de la inclinación máxima de la superficie.
Clasificación de las vertientes según Ruhe, R.V. (1975)
- Perfil en el sentido de la inclinación de la vertiente.
- Perfil en el sentido de la dirección de la vertiente.
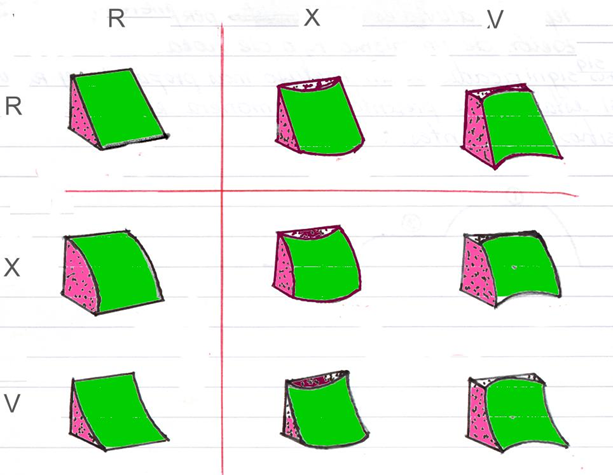
De acuerdo con la clasificación de Ruhe (1975) se puede inferir fácilmente:
- El flujo superficial y subsuperficial de agua sigue trayectorias diferentes según el tipo de vertiente. En unos casos los flujos son divergentes, en otros casos los flujos son convergentes, y en otros casos el flujo es paralelo, es decir, ni divergente, ni convergente.
- El flujo de agua en una vertiente tiene implicaciones importantes en:
- El desarrollo fisiológico de la vegetación.
- La respuesta diferencial frente a períodos húmedos o secos prolongados.
- El desarrollo de los perfiles de suelo.
- La estabilidad de las vertientes.
- La evolución de los perfiles de meteorización de las rocas.
Cálculo de la curvatura de perfil (vertical)
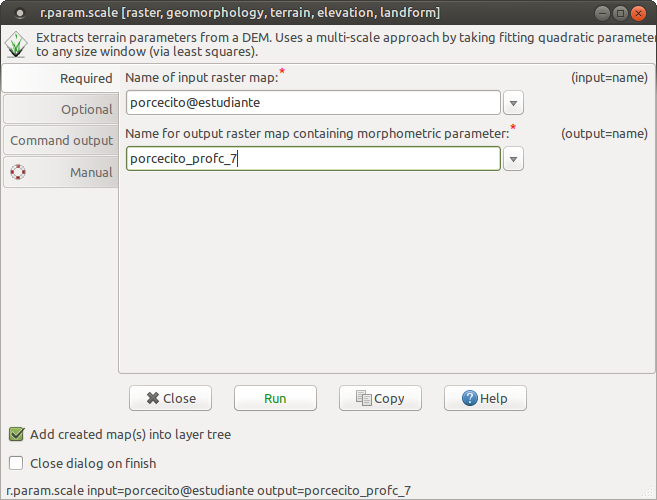
Utilizando la herramienta r.param.scale vamos a calcular el parámetro profc con una ventana móvil de procesamiento de tamaño de 7x7 pixeles, e indicamos un nombre descriptivo para el mapa que obtendremos, haciendo referencia al parámetro y al tamaño de la ventana móvil de procesamiento.
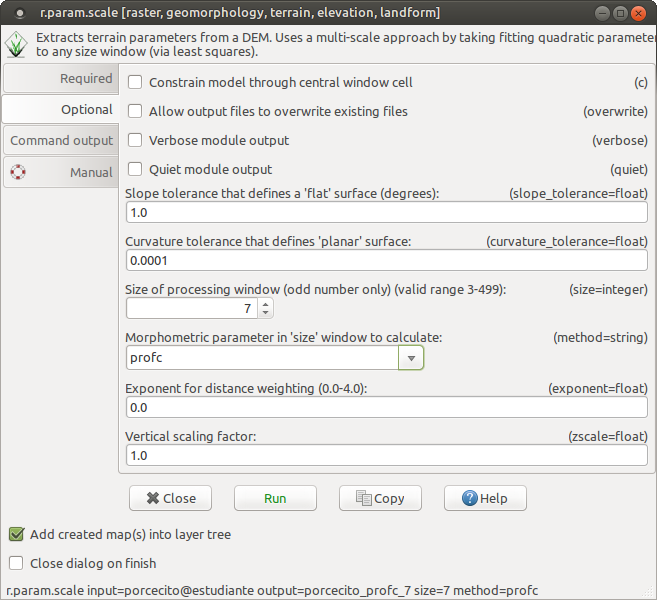
En la pestaña Optional indicamos el parámetro a extraer y el tamaño de la ventana móvil a utilizar.
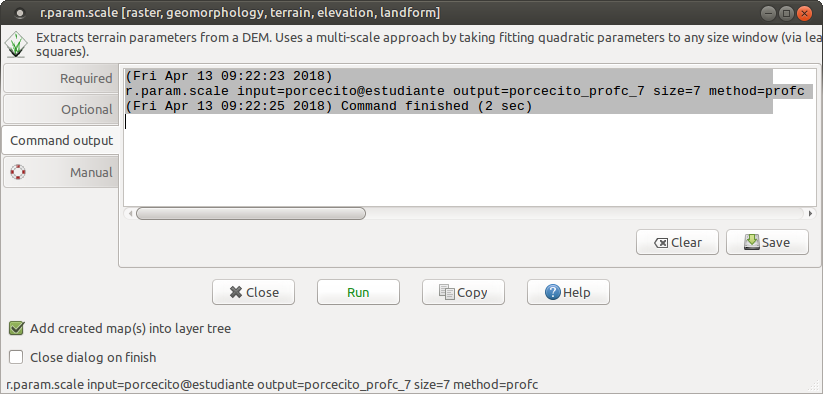
Y ejecutamos la herramienta:
Recordemos el significado de los valores positivos (curvatura convexa) y negativos (curvatura cóncava) para la curvatura vertical de acuerdo a lo definido para este parámetro al inicio de la clase:
- Los valores positivos de curvatura hacen referencia a perfiles convexos; mientras mayor sea el valor de la curvatura (más positivo), más cerrada es la convexidad.
- Los valores negativos de curvatura hacen referencia a perfiles cóncavos; mientras menor sea el valor de la curvatura (más negativo), más cerrada es la concavidad.
- Los valores cercanos a 0 hacen referencia a curvaturas muy abiertas que se aproximan a un plano; convexidades muy abiertas para valores positivos y concavidades muy abiertas para valores negativos.
El mapa de curvatura de perfil debe reclasificarse al menos en 3 categorías principales:
- Las curvaturas convexas (positivas).
- Las curvaturas planares (cercanas a 0).
- Las curvaturas cóncavas (negativas).
También se pueden emplear más rangos si se desean diferenciar las curvaturas convexas y cóncavas, entre aquellas que son muy abiertas y aquellas que son muy cerradas.
Lo primero que debemos hacer para poder llevar a cabo esta reclasificación, es consultar la información estadística del mapa obtenido.
Pero no es suficiente la estadística univariada que se obtiene de manera regular por el menú contextual de la capa, es necesario invocar la herramienta de estadística r.univar para indicar que deseamos una estadística extendida, que incluye los cuartiles y el valor correspondiente al percentil 90% de los datos.
En ella indicamos el nombre de la capa raster a la cual le deseamos obtener la estadística.
Y en la pestaña Extended activamos la opción para estadística extendida, opcionalmente acá podemos indicar cual o cuales percentiles queremos reportar.
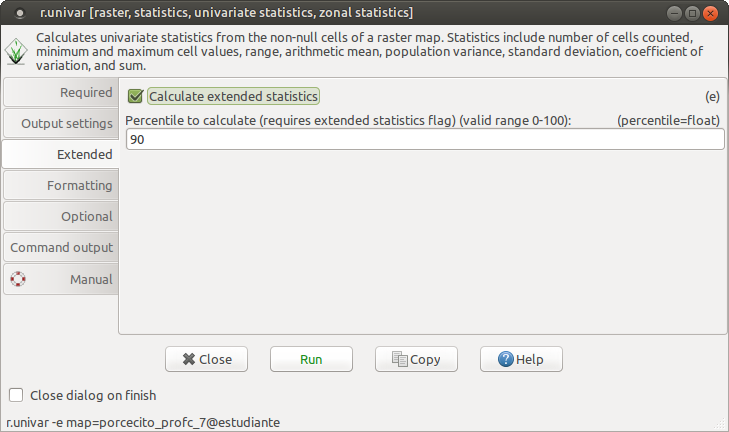
Al ejecutar la orden, obtenemos el resultado.
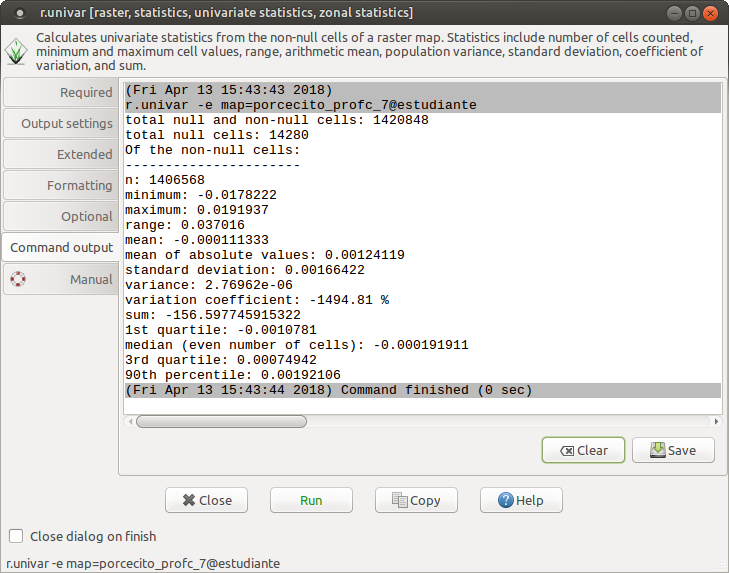
total null and non-null cells: 1420848
total null cells: 14280
Of the non-null cells:
----------------------
n: 1406568
minimum: -0.0178222
maximum: 0.0191937
range: 0.037016
mean: -0.000111333
mean of absolute values: 0.00124119
standard deviation: 0.00166422
variance: 2.76962e-06
variation coefficient: -1494.81 %
sum: -156.597745915322
1st quartile: -0.0010781
median (even number of cells): -0.000191911
3rd quartile: 0.00074942
90th percentile: 0.00192106
De acuerdo con los datos obtenidos, observamos que los valores de curvatura son extremadamente bajos, de tal modo que el valor promedio (mean) es del órden de una diezmilésima.
Para poder reclasificar este mapa, necesitamos que los valores de curvatura sean del órden de decenas a centenas, puesto que al especificar los rangos de reclasificación sólo se pueden utilizar valores enteros. Por lo que debemos escalar los valores del mapa original.
Reclasificación del mapa de curvatura de perfil
Para escalar el mapa, debemos de multiplicarlo por un factor de manera que el valor promedio sea del órden de las décimas para poder utilizar rangos enteros en la tabla de reclasificación.
Esto lo haremos por medio de la Calculadora de mapas raster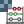 
multiplicando el mapa original por $10^5$.
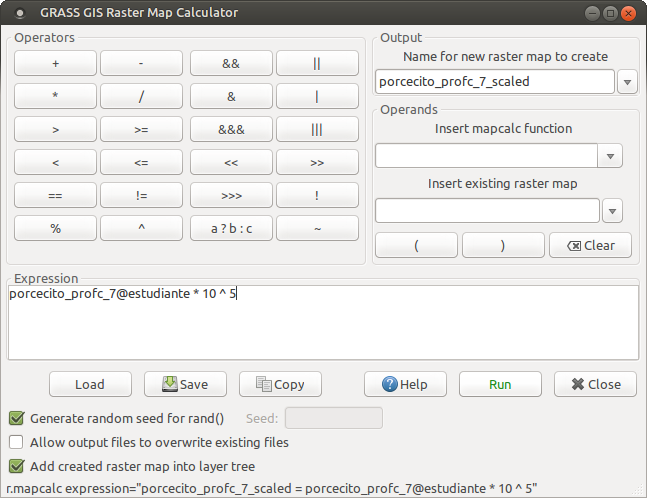
Y volvemos a calcular los estadísticos de la nueva capa para definir las reglas de reclasificación.
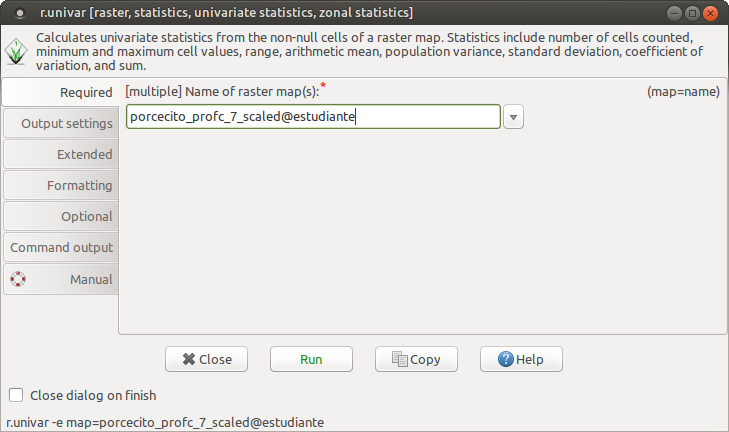
Observemos que el mapa no se está modificando drásticamente, pues sólo cambiamos la escala de sus valores, que ahora son más manejables para hacer la reclasificación. En los nuevos valores de curvatura, el promedio (mean) ya se encuentra en el órden de las decenas y podemos especificar los rangos de reclasificación.
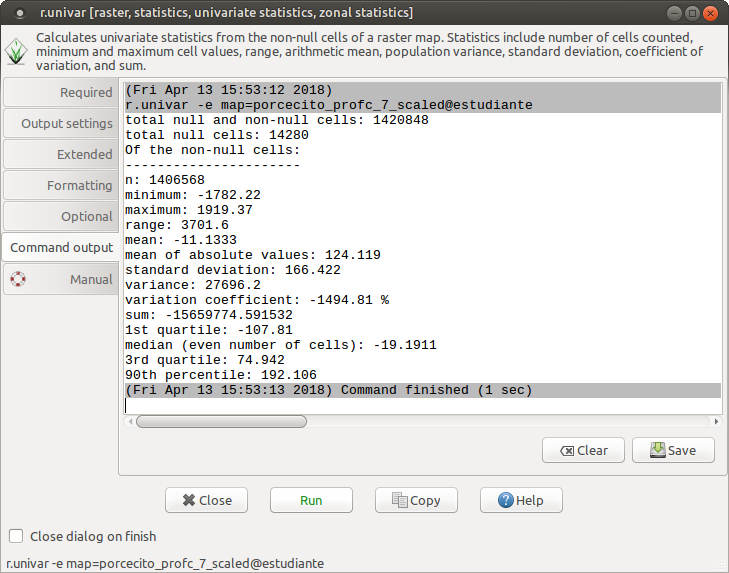
total null and non-null cells: 1420848
total null cells: 14280
Of the non-null cells:
----------------------
n: 1406568
minimum: -1782.22
maximum: 1919.37
range: 3701.6
mean: -11.1333
mean of absolute values: 124.119
standard deviation: 166.422
variance: 27696.2
variation coefficient: -1494.81 %
sum: -15659774.591532
1st quartile: -107.81
median (even number of cells): -19.1911
3rd quartile: 74.942
90th percentile: 192.106
La clasificación de las curvaturas de perfil profc y plana planc presuponen como condición necesaria un conocimiento del relieve de la región representado en el mapa. Es el conocimiento de campo el que nos permite estimar o seleccionar adecuadamente el peso de los distintos tipos de curvatura. En este sentido, el computador brinda la opción de seleccionar cualquier rango y por lo tanto, obtener un número elevado de mapas distintos. Es la experiencia de campo la que permite tener un criterio adecuado para seleccionar los pesos de los diferentes tipos de curvatura.
Para la región de Porcecito en el departamento de Antioquia, vamos a considerar que las curvaturas de perfil cóncavas tienen pesos del órden del 40%, las curvaturas rectilíneas un peso del 20% y las curvaturas convexas un peso del 40%. Esta información es la que proviene de la experiencia de campo para incorporar al análisis computacional.
Utilizando el parámetro percentile de la herramienta r.univar podemos calcular los valores correspondientes a los percentiles 40% y 60% del mapa de curvatura vertical que dividen el rango de valores en 40% - 20% - 40%.
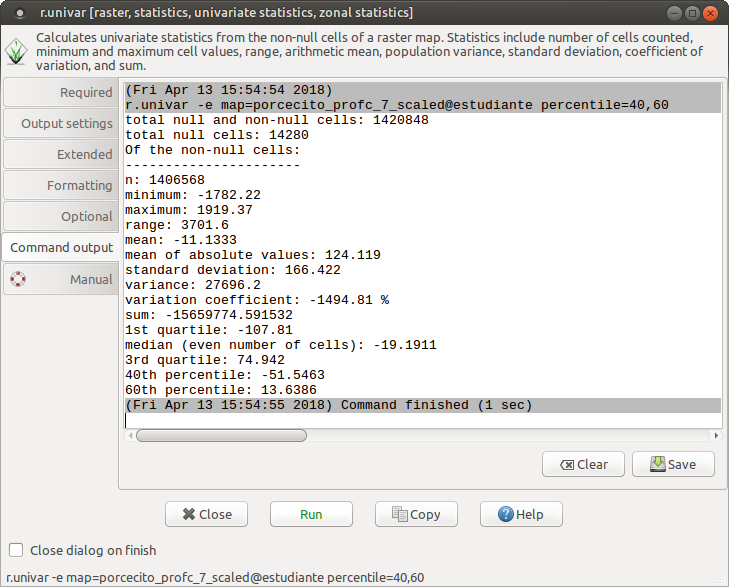
total null and non-null cells: 1420848
total null cells: 14280
Of the non-null cells:
----------------------
n: 1406568
minimum: -1782.22
maximum: 1919.37
range: 3701.6
mean: -11.1333
mean of absolute values: 124.119
standard deviation: 166.422
variance: 27696.2
variation coefficient: -1494.81 %
sum: -15659774.591532
1st quartile: -107.81
median (even number of cells): -19.1911
3rd quartile: 74.942
40th percentile: -51.5463
60th percentile: 13.6386
Puesto que la idea es que el límite sea simétrico con respecto al 0 absoluto, utilizaremos el valor promedio entre los percentiles 40 y 60 (en valor absoluto):
\[\frac{51.5463 + 13.6386}{2} = \frac{65.1849}{2} = 32.59245 \approx 33\]Las reglas de reclasificación propuestas se indican a continuación, utilizando el límite calculado tanto positivo como negativo.
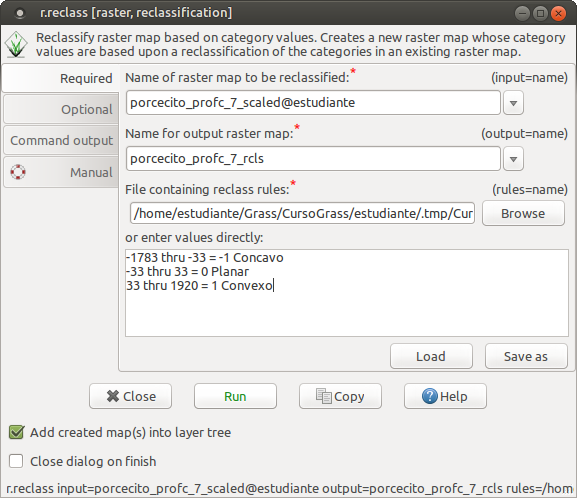
-1783 thru -33 = -1 Concavo
-33 thru 33 = 0 Planar
33 thru 1920 = 1 Convexo
El reporte de las categorías sería el siguiente:
+-----------------------------------------------------------------------------+
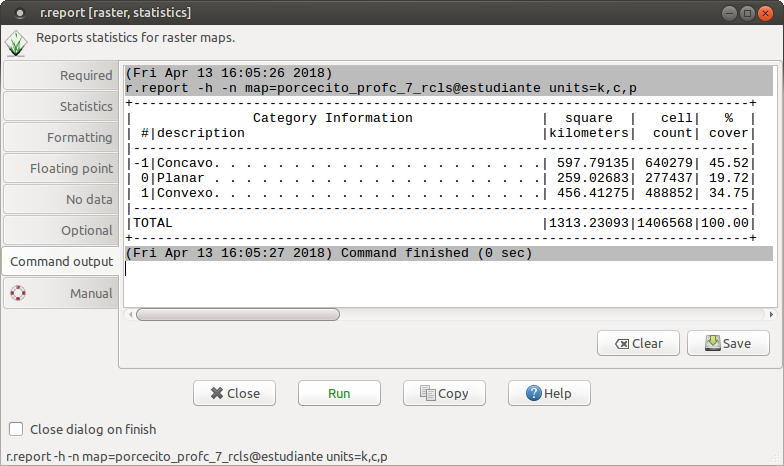
| Category Information | square | cell| % |
| #|description |kilometers| count| cover|
|-----------------------------------------------------------------------------|
|-1|Concavo. . . . . . . . . . . . . . . . . . . . .| 597.79135| 640279| 45.52|
| 0|Planar . . . . . . . . . . . . . . . . . . . . .| 259.02683| 277437| 19.72|
| 1|Convexo. . . . . . . . . . . . . . . . . . . . .| 456.41275| 488852| 34.75|
|-----------------------------------------------------------------------------|
|TOTAL |1313.23093|1406568|100.00|
+-----------------------------------------------------------------------------+
El mapa reclasificado obtenido es el siguiente:
El mapa de la curvatura vertical muestra claramente la diferencia entre concavidades pertenecientes a valles y convexidades perteneciente a divisorias de agua ubicadas en cimas de colinas.
Cálculo de la curvatura plana (horizontal)
Utilizando la herramienta r.param.scale vamos a calcular el parámetro planc con una ventana móvil de procesamiento de tamaño de 7x7 pixeles, e indicamos un nombre descriptivo para el mapa que obtendremos, haciendo referencia al parámetro y al tamaño de la ventana móvil de procesamiento.
En la pestaña Optional indicamos el parámetro a extraer y el tamaño de la ventana móvil a utilizar.
Y ejecutamos la herramienta:
Recordemos el significado de los valores positivos (curvatura cóncava) y negativos (curvatura convexa) para la curvatura horizontal de acuerdo a lo definido para este parámetro al inicio de la clase:
- Los valores positivos de curvatura hacen referencia a planos cóncavos; mientras mayor sea el valor de la curvatura (más positivo), más cerrada es la concavidad.
- Los valores negativos de curvatura hacen referencia a planos convexos; mientras menor sea el valor de la curvatura (más negativo), más cerrada es la convexidad.
- Los valores cercanos a 0 hacen referencia a curvaturas muy abiertas que se aproximan a un plano; concavidades muy abiertas para valores positivos y convexidades muy abiertas para valores negativos.
Nótese que los signos positivo y negativo tienen significado opuesto en las curvaturas plana y de perfil.
Vamos a emplear las mismas 3 categorías de curvatura para el caso de la curvatura plana:
- Las curvaturas convexas (negativas).
- Las curvaturas planares (cercanas a 0).
- Las curvaturas cóncavas (positivas).
Consultamos la estadística extendida del mapa obtenido.
Y obtenemos:
total null and non-null cells: 1420848
total null cells: 14280
Of the non-null cells:
----------------------
n: 1406568
minimum: -19.2
maximum: 12.8727
range: 32.0727
mean: -0.000110073
mean of absolute values: 0.0101302
standard deviation: 0.0325693
variance: 0.00106076
variation coefficient: -29588.7 %
sum: -154.825710731604
1st quartile: -0.00591049
median (even number of cells): -0.000227176
3rd quartile: 0.00547276
90th percentile: 0.0133584
Reclasificación del mapa de curvatura plana
De igual manera que hicimos con el mapa de curvatura de perfil debemos escalar los valores del mapa de curvatura plana porque el valor promedio (mean) es muy cercano a cero.
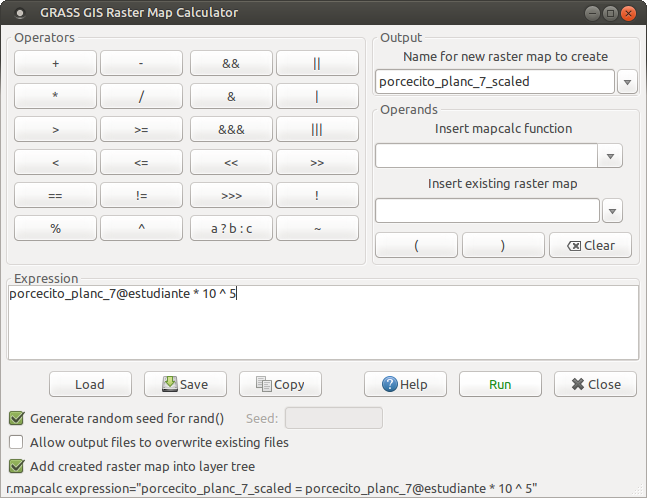
Y calculamos nuevamente los estadísticos para definir las reglas de reclasificación utilizando los mismos pesos (40% - 20% - 40%).
Y obtenemos:
total null and non-null cells: 1420848
total null cells: 14280
Of the non-null cells:
----------------------
n: 1406568
minimum: -1.92e+06
maximum: 1.28727e+06
range: 3.20727e+06
mean: -11.0073
mean of absolute values: 1013.02
standard deviation: 3256.93
variance: 1.06076e+07
variation coefficient: -29588.7 %
sum: -15482571.0731596
1st quartile: -591.049
median (even number of cells): -22.7176
3rd quartile: 547.276
40th percentile: -218.711
60th percentile: 173.238
De igual manera que con la curvatura de perfil, la idea es que el límite sea simétrico con respecto al 0 absoluto, utilizaremos el valor promedio entre los percentiles 40 y 60 (en valor absoluto):
\[\frac{218.711 + 173.238}{2} = \frac{391.949}{2} = 195.9745 \approx 196\]Las reglas de reclasificación se indican a continuación.
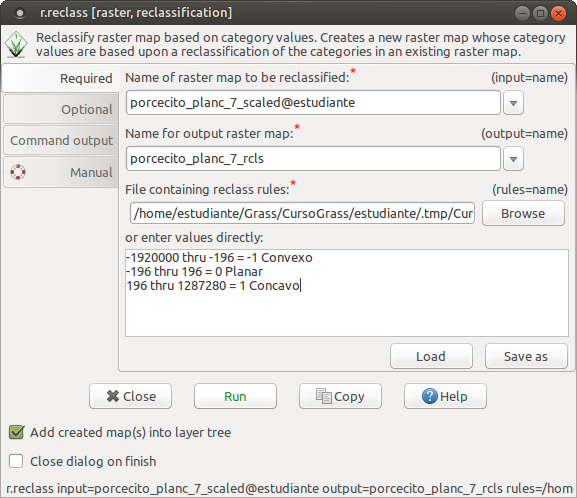
-1920000 thru -196 = -1 Convexo
-196 thru 196 = 0 Planar
196 thru 1287280 = 1 Concavo
Se reclasifica el mapa de acuerdo a las reglas definidas, y se obtiene un reporte de la distribución de las categorías.
+-----------------------------------------------------------------------------+
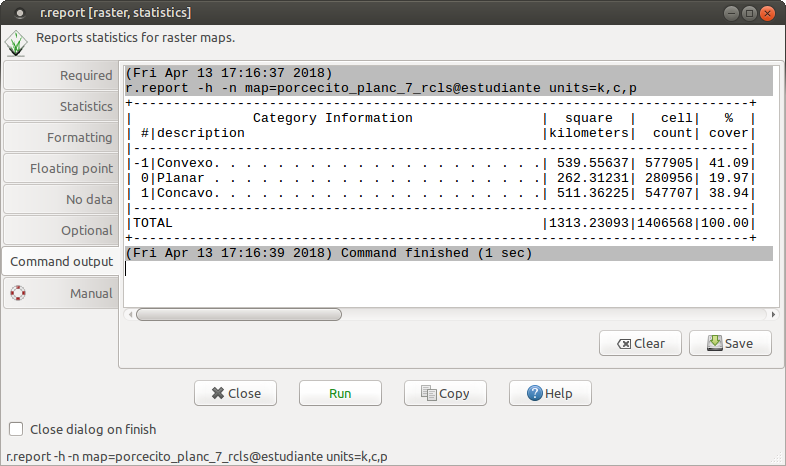
| Category Information | square | cell| % |
| #|description |kilometers| count| cover|
|-----------------------------------------------------------------------------|
|-1|Convexo. . . . . . . . . . . . . . . . . . . . .| 539.55637| 577905| 41.09|
| 0|Planar . . . . . . . . . . . . . . . . . . . . .| 262.31231| 280956| 19.97|
| 1|Concavo. . . . . . . . . . . . . . . . . . . . .| 511.36225| 547707| 38.94|
|-----------------------------------------------------------------------------|
|TOTAL |1313.23093|1406568|100.00|
+-----------------------------------------------------------------------------+
El mapa reclasificado obtenido es el siguiente:
Observar que haciendo zoom en sectores del mapa se pueden observar rasgos específicos del relieve.
Combinación de los mapas de curvaturas plana y de perfil
El mapa reclasificado de curvatura de perfil (vertical) tiene 3 valores:
| Valor | Tipo de curvatura de perfil |
|---|---|
| -1 | Concava (V) |
| 0 | Rectilínea (R) |
| 1 | Convexa (X) |
El mapa reclasificado de curvatura plana (horizontal) tiene 3 valores:
| Valor | Tipo de curvatura plana |
|---|---|
| -1 | Convexa (X) |
| 0 | Rectilínea (R) |
| 1 | Concava (V) |
Es factible combinar estos dos mapas para obtener un mapa resultante en el cual se puedan obtener simultáneamente las curvaturas plana y de perfil para cada pixel. Como cada mapa tiene 3 categorías diferentes, el mapa resultante tendrá 9 categorías (3x3). Debemos sí, garantizar que cada categoría del mapa resultante tenga un valor único. La matriz a obtener deberá ser de la siguiente manera:
| X | R | V | |
| V | VX | VR | VV |
| R | RX | RR | RV |
| X | XX | XR | XV |
En las filas están las categorías de curvatura de perfil y en las columnas las categorías de la curvatura plana.
Si sumamos los valores de los 2 mapas reclasificados, obtendríamos:
| -1 | 0 | 1 | |
| -1 | -2 | -1 | 0 |
| 0 | -1 | 0 | 1 |
| 1 | 0 | 1 | 2 |
Observemos
- La suma simple de los 2 mapas no permite diferenciar los segmentos RX de VR porque ambos tienen el mismo valor de -1.
- De igual manera sucede con los segmentos XX - RR - VV, los cuales tienen el mismo valor de 0
- También para los segmentos XR y RV, que tienen el mismo valor de 1.
Para evitar la repetición de valores, multiplicamos el mapa de curvatura plana por el escalar 3:
| -3 | 0 | 3 | |
| -1 | -4 | -1 | 2 |
| 0 | -3 | 0 | 3 |
| 1 | -2 | 1 | 4 |
En este segundo caso cada combinación quedará con un valor diferente:
| Valor | Tipo de vertiente |
|---|---|
| -4 | VX |
| -3 | RX |
| -2 | XX |
| -1 | VR |
| 0 | RR |
| 1 | XR |
| 2 | VV |
| 3 | RV |
| 4 | XV |
De modo que utilizando el álgebra de mapas podemos obtener el mapa mediante la operación:
tipo_vert = profc + planc * 3
La cual podemos efectuar utilizando la Calculadora de mapas raster .
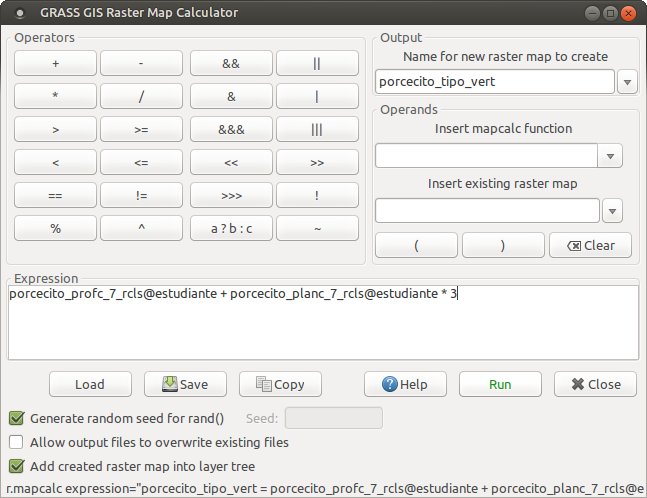
Visualizamos la distribución de los tipos de vertientes en el mapa porcecito_tipo_vert:
+-----------------------------------------------------------------------------+
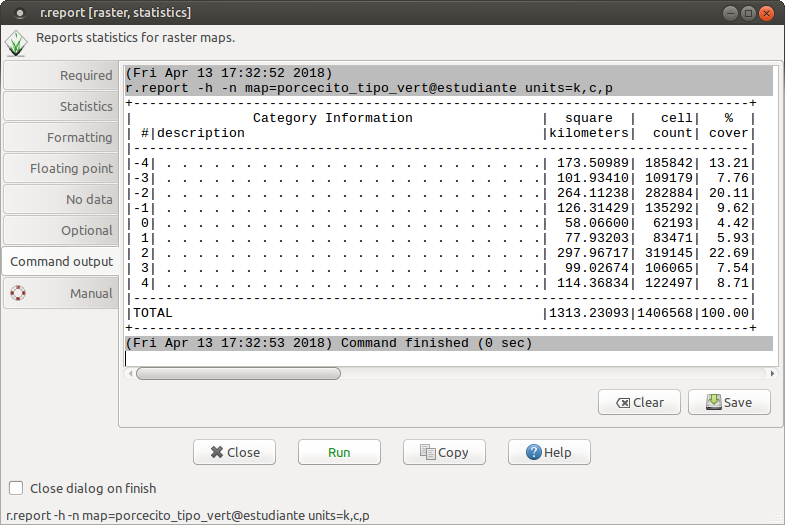
| Category Information | square | cell| % |
| #|description |kilometers| count| cover|
|-----------------------------------------------------------------------------|
|-4| . . . . . . . . . . . . . . . . . . . . . . . .| 173.50989| 185842| 13.21|
|-3| . . . . . . . . . . . . . . . . . . . . . . . .| 101.93410| 109179| 7.76|
|-2| . . . . . . . . . . . . . . . . . . . . . . . .| 264.11238| 282884| 20.11|
|-1| . . . . . . . . . . . . . . . . . . . . . . . .| 126.31429| 135292| 9.62|
| 0| . . . . . . . . . . . . . . . . . . . . . . . .| 58.06600| 62193| 4.42|
| 1| . . . . . . . . . . . . . . . . . . . . . . . .| 77.93203| 83471| 5.93|
| 2| . . . . . . . . . . . . . . . . . . . . . . . .| 297.96717| 319145| 22.69|
| 3| . . . . . . . . . . . . . . . . . . . . . . . .| 99.02674| 106065| 7.54|
| 4| . . . . . . . . . . . . . . . . . . . . . . . .| 114.36834| 122497| 8.71|
|-----------------------------------------------------------------------------|
|TOTAL |1313.23093|1406568|100.00|
+-----------------------------------------------------------------------------+
Para asignarle etiquetas a las categorías del nuevo mapa, utilizamos la herramienta r.category que abrimos desde el menú Raster -> Change category values and labels -> Manage category information.
En la herramienta seleccionamos el mapa de tipos de vertiente.
Y en la pestaña Define especificamos las etiquetas de las categorías indicando el valor de la categoría separando la etiqueta con una tabulación.
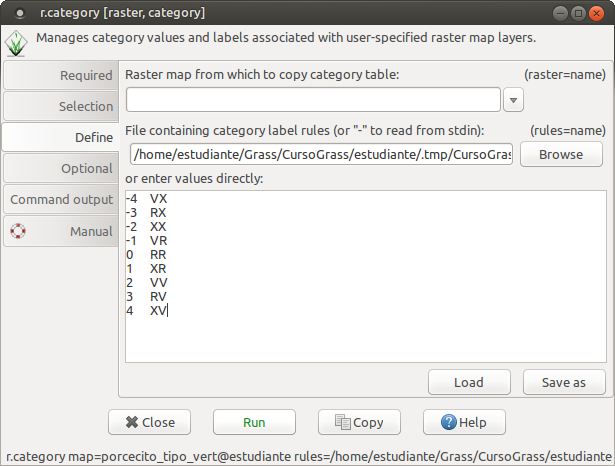
-4 VX
-3 RX
-2 XX
-1 VR
0 RR
1 XR
2 VV
3 RV
4 XV
Consultamos la distribución nuevamente:
+-----------------------------------------------------------------------------+
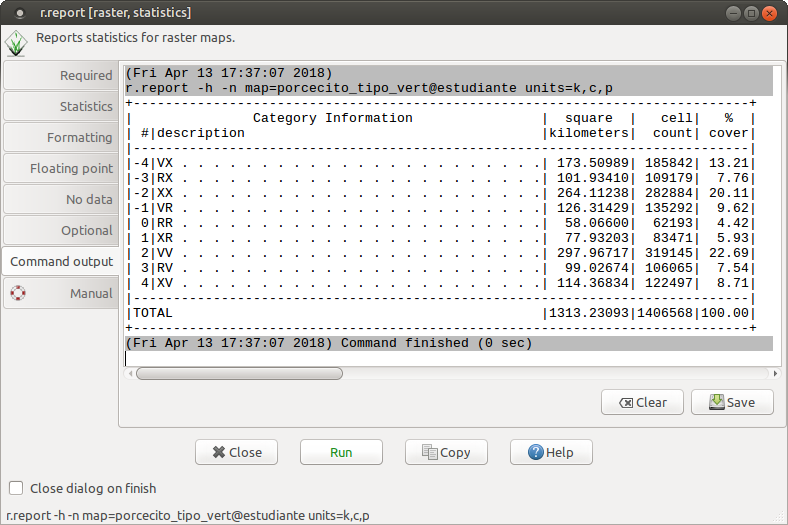
| Category Information | square | cell| % |
| #|description |kilometers| count| cover|
|-----------------------------------------------------------------------------|
|-4|VX . . . . . . . . . . . . . . . . . . . . . . .| 173.50989| 185842| 13.21|
|-3|RX . . . . . . . . . . . . . . . . . . . . . . .| 101.93410| 109179| 7.76|
|-2|XX . . . . . . . . . . . . . . . . . . . . . . .| 264.11238| 282884| 20.11|
|-1|VR . . . . . . . . . . . . . . . . . . . . . . .| 126.31429| 135292| 9.62|
| 0|RR . . . . . . . . . . . . . . . . . . . . . . .| 58.06600| 62193| 4.42|
| 1|XR . . . . . . . . . . . . . . . . . . . . . . .| 77.93203| 83471| 5.93|
| 2|VV . . . . . . . . . . . . . . . . . . . . . . .| 297.96717| 319145| 22.69|
| 3|RV . . . . . . . . . . . . . . . . . . . . . . .| 99.02674| 106065| 7.54|
| 4|XV . . . . . . . . . . . . . . . . . . . . . . .| 114.36834| 122497| 8.71|
|-----------------------------------------------------------------------------|
|TOTAL |1313.23093|1406568|100.00|
+-----------------------------------------------------------------------------+
Y ya las categorías pueden ser identificadas.